Gün 4
Merhaba Zeynep! Şimdiye kadar doğrusal ve ikinci dereceden fonksiyonları gördük. Bugün ise SAT'de karşına çıkabilecek bazı özel ve ilginç fonksiyon türlerine göz atacağız: Mutlak değer, üstel ve trigonometrik fonksiyonlar.
Bölüm 1: Mutlak Değer Fonksiyonu f(x) = |x|
Mutlak değer, bir sayının sıfıra olan uzaklığıdır. Uzaklık her zaman pozitif olduğu için, mutlak değer de her zaman pozitif veya sıfırdır.
|5| = 5|-5| = 5
Mutlak değer fonksiyonunun grafiği 'V' şeklindedir. Negatif y değerleri almaz.
Zeynep'e SAT İpucu!
|x - 2| = 5 ise, bu demektir ki:1)
x - 2 = 5 (yani x = 7)2)
x - 2 = -5 (yani x = -3)Her zaman iki olasılığı da kontrol et!
Bölüm 2: Üstel Fonksiyonlar (Exponential Functions)
Değişkenin ('x') üs olarak yer aldığı fonksiyonlardır. Formülü f(x) = bˣ şeklindedir, burada 'b' tabandır ve pozitif bir sayıdır.
Üstel fonksiyonlar, bakteri popülasyonu, faizle para biriktirme gibi "hızlı büyüme" veya radyoaktif bozunma gibi "hızlı küçülme" durumlarını modeller.
Örnek: f(x) = 2ˣ
Grafikten de görebileceğin gibi, x arttıkça y değeri çok daha hızlı bir şekilde artar. Bu fonksiyon asla 0 veya negatif bir değer almaz.
Bölüm 3: Trigonometrik Fonksiyonlar (Sinüs ve Kosinüs)
Trigonometrik fonksiyonlar, genellikle dik üçgenlerdeki kenar oranları veya birim çember üzerindeki hareketle ilişkilidir. SAT'de genellikle temel sinüs (sin) ve kosinüs (cos) fonksiyonları ile karşılaşırsın.
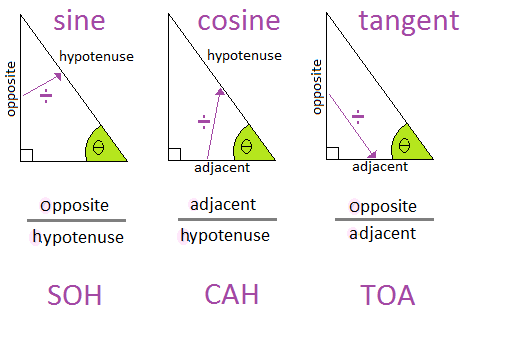
- Sinüs (sin): Karşı Kenar / Hipotenüs
- Kosinüs (cos): Komşu Kenar / Hipotenüs
Bu fonksiyonların grafikleri, kendini tekrar eden periyodik dalgalardır. Ses dalgaları, salıncak hareketi gibi tekrarlayan olayları modellerler.
Zeynep'e SAT İpucu!
Bugün fonksiyonlar dünyasının daha özel üyeleriyle tanıştık. Mutlak değerin 'V' şekli, üstel fonksiyonların hızlı yükselişi ve trigonometrinin periyodik dalgaları aklında kalsın. Yarın tüm bu öğrendiklerimizi gerçek SAT tarzı uygulama sorularıyla pekiştireceğiz!
1. |2x - 3| = 7 denkleminin çözüm kümesi aşağıdakilerden hangisidir?
2. f(x) = 3ˣ fonksiyonu için f(3) değeri kaçtır?
3. Aşağıdaki durumlardan hangisi en iyi üstel bir fonksiyonla modellenebilir?
4. f(x) = |x - 4| fonksiyonunun alabileceği en küçük değer nedir?